一、基本公式
首先，我们要明确年均增长中最核心的两个公式：
注：初期值是指一个时间段内的第一年；末期值是指一个时间段内的最后一年；n是指增长次数(通常用年份差来代替)。
二、常见考点
考点一：有关年均增长量公式的考查。
具体来说，常考已知年均增长量和初期值，求末期值。或者，已知年均增长量和末期值，求初期值等。
【例1】2013年我国建筑业总产值160366亿元，2013—2018年平均每年增加14944亿元。
问题：2018年我国建筑业总产值是多少亿元？
A.235086
B.247743
C.256672
D.254324
答案：A。
【解析】此题求解末期值，根据公式末期值=初期值+n×年均增长量，即总产值=160366+5×14944，观察选项末一位数字不同，故只需计算末一位即可。6+0尾数为6。选择A选项。
考点二：比较年均增长率的大小
一般情况下，题目会要求在年份差相同的情况下，比较年均增长率的大小，我们只需要直接比较
的大小即可。
【例2】
问题：1995-2015年受教育程度人数平均增速最快的人群是：
A.大学
B.高中
C.初中
D.小学
答案：A
【解析】题干比较的是年均增长率的大小，且比较的时间段都是1995-2015年，年份差一致，故直接比较即可；四个选项分别为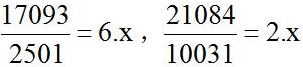
，
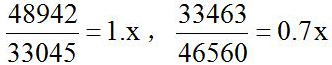。选择A选项。
考点三：按一定的年均增速求末期值
【例3】2014—2018年，我国居民消费水平分别为17778元、19397元、21285元、22935元、25002元。
问题：如果2018年以后每年的年均增速都按照2014—2018年的年均增速来计算，求2022年我国居民消费水平将达到多少元？
A.29432
B.35161
C.39012
D.45621
答案：B
【解析】题干求末期值，根据公式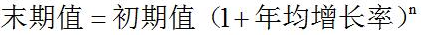
，即以2018年的25002元为初期值，2014-2018年的年均增长率为
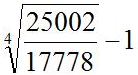，代入公式即为
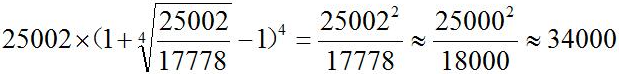。答案选择B。
